KV熵的Blog

题目传送门

（本蒟蒻也是看到了这篇题解，才想看出来的）。

题目内容较为简单，选出由$(1,1)$到$(m,n)$（此路径只能往下或往右）和由$(m,n)$到$(1,1)$路径（此路径只能往左或往上），并保证这两条路径没有交点（除起点和终点外），同时还要保证这两条路径的好感度之和最大。我们可以对此问题进行转化：找到两条由$(1,1)$到$(m,n)$的路径，并保证这两条路径没有交点（除起点和终点外）。我们随便画一条路径（这是原题解的那张图片）。

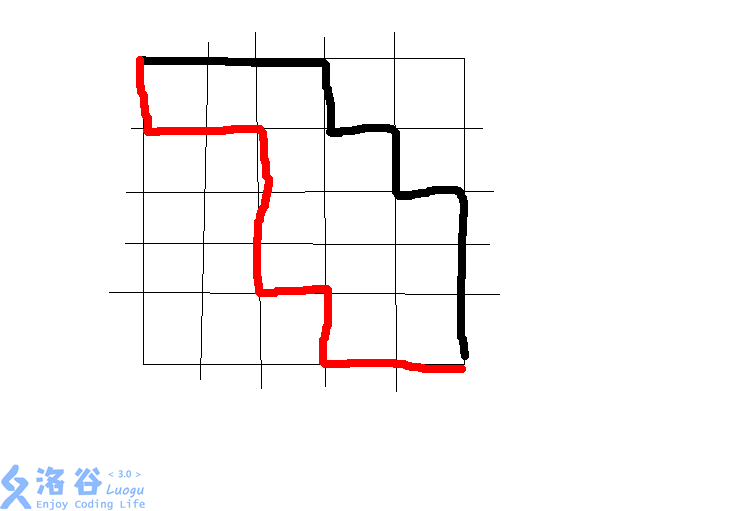
现在我们称红色路径为r路径，黑色路径为b路径。

可以发现r路径始终在b路径的左下方，b路径始终在r路径的右上方。同时，也不难推测，两条路径一定由一条路径在左下方，一条路径在右上方的。

接下来，我们需要构建dp，我们令$dp_{i,j,k,l}$表示终点为$(i,j)$和终点为$(k,l)$的两条路径的好感读的最大值。我们可以让终点为$(k,l)$的路径位于左下方，则$k>i,l<j$。其余的动态转移方程其实并不复杂：$dp_{i,j,k,l} = max(dp_{i-1,j,k-1,l},dp_{i-1,j,k,l-1},dp_{i,j-1,k-1,l},dp_{i,j-1,k,l-1})+a_{i,j}+a_{k,l}$。不过$k>i,l<j$的话dp是走不到终点的，最后答案在$dp_{m-1,n,m,n-1}$

好的，然后就可以上代码了：

#include<bits/stdc++.h>

using namespace std;

const int N = 60;
int a[N][N],dp[N][N][N][N];

int main(){
	int m,n;
	cin >> m >> n;
	for(int i = 1;i <= m;i++){
		for(int j = 1;j <= n;j++){
			cin >> a[i][j];
		}
	}
	for(int i = 1;i <= m;i++){
		for(int j = 1;j <= n;j++){
			for(int k = i+1;k <= m;k++){
				for(int l = 1;l < j;l++){
					dp[i][j][k][l] = max({dp[i-1][j][k-1][l],dp[i-1][j][k][l-1],dp[i][j-1][k-1][l],dp[i][j-1][k][l-1]})+a[i][j]+a[k][l];
				}
			}
		}
	}
	cout << dp[m-1][n][m][n-1];
	return 0;
}